◈ 소리와 주파수
  

1. 주파수 (Frequency)

  ◇ 주파수란?

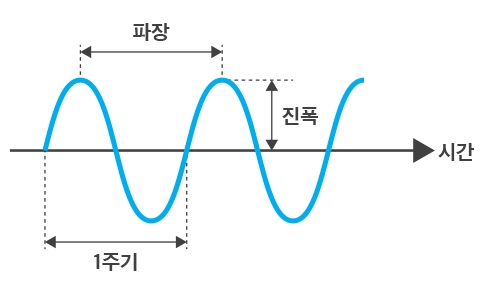
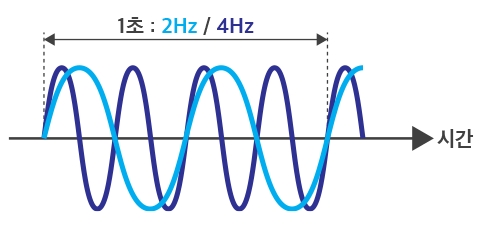
파동이 1초 동안 반복되는 횟수 즉 진동수를 말합니다. 단위는 Hz 라고 하는데, 이는 독일 물리학자 하인리히 루돌프 헤르츠의 이름을 기리기 위한 것입니다. 1 Hz는 1초 동안 파동이 1회 진행됨을 말합니다. 2Hz, 4Hz 라면 1초 동안 2회, 4회 반복되었음을 말합니다. (1 KHz 라는 것은 1,000 번 이라는 것을 말합니다. [그림 2] 참조)

파동은 진폭과 주기로 특정할 수 있으며, 주기가 정해지면 주파수와 파장은 자동으로 계산 되어진다.

- 진폭 : 파동의 크기, 즉 소리의 크기

- 주기 : 파동이 1 Cycle 진행하는데 소요된 시간

- 주파수 : 1초 동안 파동이 진행된 Cycle 수
              소리의 음정(음높이)을 나타냄

- 파장 : 파동이 1회 진행되는 동안 진행된 거리

[▲ 그림 1]

  ◇ 소리(Sound)는 진동(Vibrayion)에 의해 형성되어
       파동(Wave)의의 형태로 전달됩니다.

  ◇ 소리의 주파수 특성

[▲ 그림 2]

소리는 파동을 일으키며 그 진동이 공기를 통하여 전달되므로 모든 소리는 주파수로 분석할 수 있습니다. 낮은 소리는 주파수가 낮고, 높은 소리는 주파수가 높은 것입니다. 작은 큰 소리는 진폭이 작고, 큰 소리는 진폭이 큰 것입니다.

  ◇ 가청주파수
 

  인간의 귀는 모든 주파수에 해당하는 소리를 전부 들을 수 있는 것은 아닙니다. 컴컴한 동굴 속을 자유자재로 날아다니는 박쥐는 우리 귀에 들리지 않는 소리(초음파)의 반사를 감지하여 장애물을 피해서 비행하고 있다는 것을 우리는 알고 있습니다. 또한 아무 소리도 들리지 않았는데 집을 지키던 개가 벌떡 일어나서 낯선 사람의 접근사실을 알고서 으르렁거리던 것을 기억할 것입니다. 이러한 현상들은 각 동물마다 들을수 있는 주파수 구간이 다르고 사람이 들을 수 있는 주파수 구간의 한계가 있다는 것입니다. 가청 주파수는 사람이 귀로 느낄 수 있는 소리의 주파수 영역을 말하며 16 ~ 20,000Hz 주파수 영역을 말합니다.

   아무리 뛰어난 청력의 소유자일지라도 인식할 수 있는 음정(음의 높이)의 한계를 말하는 것입니다. 일상적인 대화는 250 ~ 2,000 Hz 구간에 속하고, 4,000 Hz 구간에서 청각 감도가 가장 좋다고 알려져 있습니다.

  ◇ 주파수별 음성에너지와 어음이해도의 분포

2. 데시벨 (deci-Bell : dB)

  ◇ 소리의 크기는 기준음압과 측정음압 사이의 상대적인 강도로 표시하며,
       힘 or 에너지(I)와 압력(P)의 비율을 나타내는 dB SPL (sound pressure level)을  단위로 사용합니다

        힘 or  에너지 dB = 10 log (I / I。)  = 10 log (P² / P。²) = 10 log (P / P。)²
        압력 dB              = 20 log (P / P。)   ※ P : 측정음압,   P。: 기준음압 

소리의 크기는 절대값으로 표현할 수 없습니다. 건청인이 들을 수 있는 가장 작은 소리를 0 dB SPL (Sound Pessure Level) 이라 정의하고, 이를 기준으로 비교하여 상대적 크기를 상용대수(Log) 값으로 나타냅니다.
사람이 들을 수 있는 가장 작은 소리를 0 Bell, 1M 떨어진 곳에서 대화하는 소리 6 Bell, 매우 씨끄러운 소리를 12 Bell 이라합니다. 이렇게 했을 때 숫자 간격이 너무 좁아서 수 많은 소리를 구분하기에 어려움이 발생합니다. 그래서 숫자값은 10배로 크게 하고, 단위는 1/10로 줄여서 표현하기로 한 것입니다. 즉 1/10을 의미하는 단위 deci를 Bell과 합하여 deciBell이라고 표현하고, 줄여서 dB라고 쓰기로 한 것입니다.

  ◇ dB SPL (sound Pressure Level) : 소리의 압력을 측청할 때 사용하는 단위

  ◇ dB HL (Hearing Level) : 사람이 들을 수 있는 청력의 크기를 표시하는 단위

  ◇ dB SL (Sensation Level) : 개인의 청력역치를 기준으로 들을 수 있는 청력의 크기를 표시하는 단위

문제 1) 소리음압(SPL)이 2배로 커졌다면 몇 dB가 증가할까요?

20 log (P/P。) => 20 log (2) =>  20 X 0.3010 = 6.02 
∴ 대략 6 dB 증가합니다.

문제 2) 소리가 20 dB SPL 차이라면 10진수로 하면 얼마나 차이가 날까요?

20 dB = 20 log (P/P。)
P/P。= 10  　∴ P = 10 X P。즉, 10배의 차이 입니다.

문제 3) 소리가 40 dB SPL 차이라면 10진수로 하면 얼마나 차이가 날까요?

20 dB + 20 dB = 40 dB    (상용로그로는 덧셈)
   10배 X 10배 = 100배     (십진수로는 곱셈)
   10², 즉 100배 차이가 난다 할 수 있습니다.

문제 4) 소리크기를 굳이 상용대수로 표시하는 이유는 무엇일까요?

어떤 수치들이 너무 큰 값 이어서 직관적인 느낌이 없을 때
유의미한 적은 값으로 치환하여 표현할 목적으로 대수(log)값으로 표현하는 것입니다.